音律

上一章声音 我们已经清楚是如何听到声音，本章讲解如何通过一根琴弦获取制作乐器的多种音，制作音律，并阐述音律的发展过程。

1.耳朵可区分的声音

上一章我们讲到人类的耳朵能听到频率20-20000之间的声音，那么频率分别为20和21耳朵能区分吗？100和101、1000和1001、10000和10001能区分吗？

根据统计表明，大部分人能区分频率差异为5%及以上的音，也就是说频率21比20刚好多5%（(21-20)/20=5%），但是101和101相差1%、1000和1001相差0.1%、10000和10001相差0.01%无法区分。频率100下一个音至少频率为105方可被耳朵区分。

制作乐器固定音之间频率差异比例低于5%的，否则弹奏时不知道该弹哪个，听众听起来无法区分浪费乐器键位。

普通人的耳朵可区分的声音的频率差异比率要在5%以上。

2.频率翻倍听感相似

如下图所示，古人把一根金属线一端固定，另一端通过一个金属底座H'后用通过滑轮绑定一个固定重量的锤，用手拉一下H和H'之间的金属线，会发出拉动吉他琴弦一样的声音，H和H'之间的金属线在振动。

我们移动金属底座H'让弹奏振动的琴弦短一些，再用手拉一下，会发出一个不同的声音。

假如琴弦是100cm，每次向左移动5cm，每次的声音都会不一样，但是我们会发现一个奇怪一个现象，当我们向左移动50cm剩50cm时候，发出的声音和100cm有点相似。同样只剩下25cm时候，声音和50cm、100cm长度也很相似。

同样90cm声音和45cm的声音也很相似，80cm声音和40cm声音也很相似，于是我们得出一个结论：琴弦向左移动一半的情况下声音类似，具体情况就是常说的升高一个八度。

那么我们只需要研究100cm到50cm里面的声音的种类，然后向左移动或者增长一倍就能获得相似的声音。

3.选择音的规则

音乐是平衡的艺术，完全和谐（种类太少）的音乐味如嚼蜡，完全不和谐的音乐像是噪音。从里面怎么选多少种声音作为音乐的基本声音，我们需要：

1. 种类不能太少，太少的话没太多变化；
2. 也不能太多，音太多耳朵也不易区分声音的差别，大部分人在声音的频率差别超过5%才能分辨；每次增长5%，两倍内最多有14个音。
3. 制作规则比较简单。

4.五度相生律 & 三分损益法

古代的希腊和中国以及其他地方的古人都发现每次在现有长度上向左移动1/3，向左移动后如果低于50cm就让它增长一倍落到100到50cm这个区间里面，则长度增加一倍。 下图列出七个音的向左移动方式，绿色表示拨片，第一次向左移动一半，听感类似，第二次向左移动1/3剩下的频率为3/2， 第三次向左移动1/3后低于50cm则增长一倍，以此一直类推。

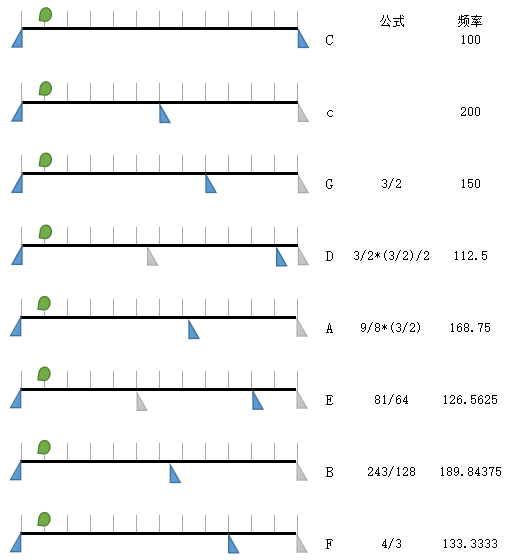
巧合的是，按照这个规则执行12次，得到的声音又会和第一个100cm类似，这12种声音分布比较均匀，种类足够，满足要求1。 制作规则也比较简单，满足要求3。

每次向左移动1/3，在物理上的振动频率上会增长到1.5倍，假如第一个音我们命名为C频率为100， 那么根据规则第二个的频率为150，第三个音频率为112.5，以此类推会得到如下表。

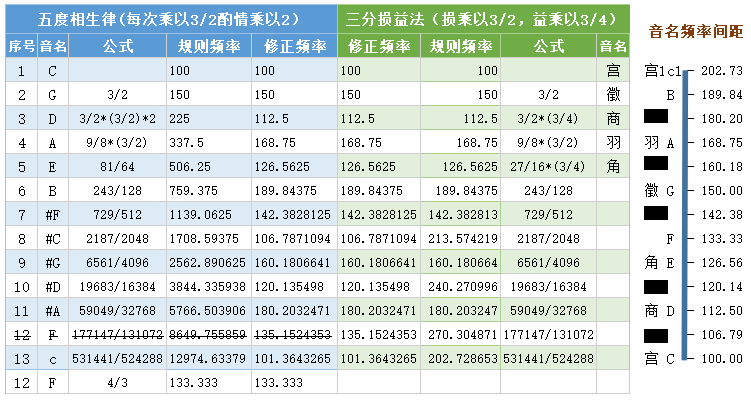
现代的弦乐器和钢琴都是用这种方式做出来的，如下图所示的吉他，通过左手按压琴弦控制左侧下弦枕到右侧品柱之间可震动的琴弦长度，弹奏出不同的音高。 假定整个长度的音高为C，到1/2之处按照上述规律分出12格做出12种音高。

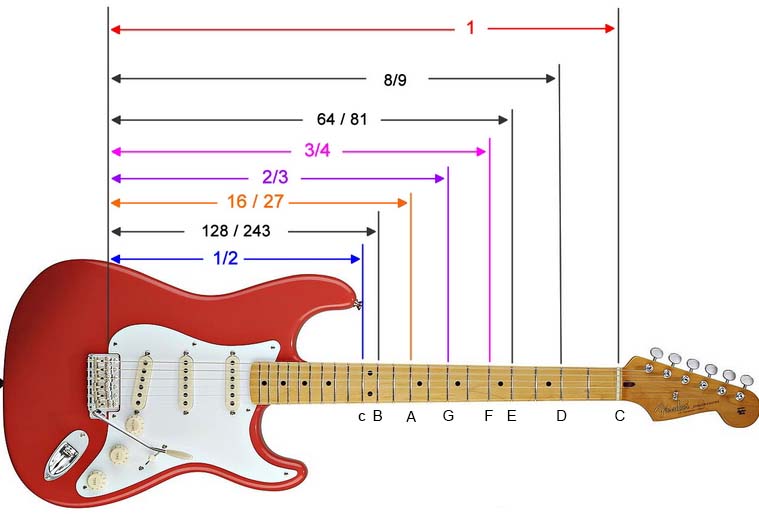
自然音

就是12种声音太多了一点，都用上感觉有点不大和谐（协和）。

古希腊选择了7个声音来做音乐，为前6个声音和第12个声音，其中第12个声音和向左移动1/4（30cm）比较接近，为制作方便就直接用前6个声音和向左移动1/4的声音。

400         506.25                       759.375 800
 |            |                             |     |
200   225     |                  337.5      |    400
 |     |      |                    |        |     |
100  112.5  126.56  133.33  150  168.75  189.84  200
 |                     |                          |
50                  66.66                        100
1      3       5       7     2     4       6      1'
C      D       E       F     G     A       B      c

我们获得了一个7个音，最初很多音乐以第六个音为主音，并使用英文ABcdefg给他们命名（小调），后来很多歌曲以第一个音为主音，为了兼容之前的歌曲使用采用CDEFGAB（大调）。 第一个音和第六个音在7个自然音排列下会有不同的调式，具体可以参看 第四章调

神奇的7：西方选择7音是目前人脑能直观记忆的个数, 最早的三字经每句三个字，诗经每句四个字，诗歌最初每句五个字后来扩展到七个字，七个字以上的就没有那么脍炙人口了，不好记。

一半琴弦长度的c比全琴弦的C音高对比用乐理名词就是高八度，度表示从CDEFGABc有8个音，高八度是西方音乐的说法。如果按照中国宫商角徵羽五音，则是高六度。目前通常流向的是西方音乐相关术语。

中国选择了前5个声音来做音乐，也就是我们熟悉的宫商角徵羽，中国称为三分损益法， 三分损益法是损时剪掉当前长度1/3,益时增加当前长度的1/3。下图CDEGA对应宫商角徵羽。

中国也有古代也有使用7音，即增加变角F和变宫B。

西方使用7音和中国使用5音的区别推测：古希腊乐器常用里拉琴（弦乐器）和奥洛斯（管乐器）祭祀，都可以手动控制消音。 而中国古代皇家祭祀乐器为编钟，无法手动消音，相当于多种音会同时发声，为了避免听起来不协和而减少音的种类。

中国对数字五有特殊爱好，手指五个很多事物喜欢凑成五：五行、五脏、五音、五味、五官、五谷等，五音还和五行对应起来：角为木，徵为火，宫为土，商为金，羽为水。

5.音组 & 国际音高

对于上述的吉他可以在50cm到25cm按照上面的规律又可以得到7个音，这个7个音比前七个音高一倍，用西方音乐术语说是高八度，因为是从C到c（CDEFGABc）中间共包含八个音。我们将这7个音命名为cdefgab。这一组一组的音，我们称为音组。

25cm到12.5cm再往下手指没有足够的空间按压，古人又发现琴弦的粗细也可以得到通用的效果。

我们可以看到吉他6根不同粗细的琴弦，通过左手手指按压控制发声的琴弦长度。

而钢琴每一个键对应一根粗细或长短不同的琴弦，每根琴弦有一个小琴槌在按键盘时敲击琴弦发出声音。可以观看视频看看钢琴原理：

现代钢琴有7个八度加4键（7x12=84）+（a4#a4b4c4)=88个键盘，其中白键为12个键中选中的7个音，黑键为12个键中未选中的5个音，所以白键为(7x7+3)=52个键盘，黑键为(7x5+1)=36个键。

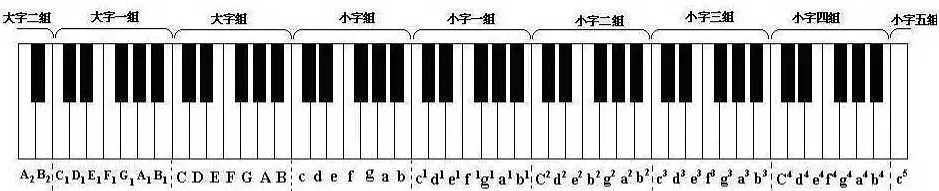
根据统计最常用的调式为C大调和A小调，对应的音高最常用为C和A，那么增加A、A#、B、C4个键差不多又多兼容了一个音组。

钢琴最左侧的白键频率（推拉耳膜）为27.5赫兹（次每秒），略高于人耳能听到的频率， 每8个白键频率升高一倍，倒数第三个白键为(27.5x2x2x2x2x2x2x2=3520)赫兹， 最右侧的白键的频率(3520x1.05946x1.05946x1.05946=4186)赫兹。

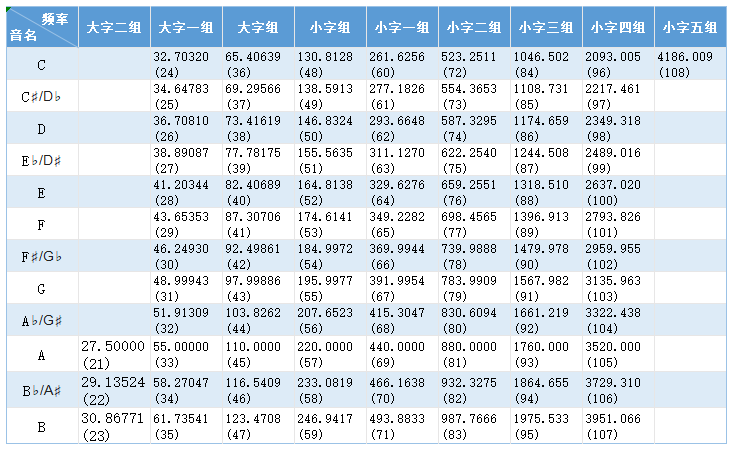
西方古人很早就能用一根琴弦完成了7个音（中国5音），此后漫长的时间内乐曲均使用7个音，这7个音也被称为 自然音。

西方在巴洛克时期（公元1600年-1750年），喜欢同时按几个键混合声音，也称为和弦，如果把其中几个音的琴弦微调一下，和弦听起来就会和谐很多。下一节我们简单讨论一下纯率。纯率以及后来出现的十二平均律均是技术逐步成熟之后的修正音律，并非原始自然音律，所以五度相生律产生的音阶就是自然音阶。修正音律包括纯率和十二平均律，也可以直接读本章小结回头再来阅读纯率和十二平均律。

6.纯率

巴洛克时期（公元1600年-1750年），西方音乐喜欢喜欢同时按几个键混合声音，发现同时弹奏CG比同时弹奏CD听起来和谐。

在两千多年前古希腊的毕达哥拉斯就发现弦长的比例最大公约数越小，先后或者同时弹奏越和谐，根据五度相生律，C和G的琴弦长度比是3:2，C和F的琴弦长度比是4:3，C和D的琴弦比为9:8，听起来和谐程度越来越低。

这个用现代声音推拉耳膜的方式也可以理解，假如声音C用每秒1次的频率推拉耳膜， 声音G用每2秒秒推拉3次的频率推拉耳膜，耳朵会感觉每两秒钟中内会推拉重的1次下1次会快速的推拉三小下， 这么有规律的方式，耳膜就会觉得和谐（协和）。

声音C用每秒1次的频率推拉耳膜，声音F用3秒4次推拉耳膜，那么耳膜感觉每4秒钟进行重复，也比较和谐（协和）。

比如C和E的弦长比是81:64(1.265625)，对于耳膜来说，需要很长时间才能发现它们的规律，听起来没那么和谐（协和）。 如果稍稍移动将它变成5:4(1.25)，那么听起来悦耳很多。 于是在巴洛克时期，由于很多乐曲使用和弦，于是在五度相生律修正成 纯率， 7个自然音如E的比率从81/64变成5/4，A的比率从27/16(1.6875)变成 5/3(1.666)，B的比率从243/128(1.8984375)变成15/8(1.8877)。

C      D       E       F     G     A       B      c
1     9/8    81/64    4/3   3/2  27/16  243/128   2  五度相生律
1     9/8     5/4     4/3   3/2   5/3     15/8    2  纯率

使用纯率的乐器虽然弹奏和弦比较和谐，但是存在几个问题：

• 从C到D是频率比是9/8，从D到E的频率比是5/4*8/9=10/9，于是5个全音会出现大全音（CD、FG、AB）和小全音（DE、GA）。
• 从E到F的频率比是16/15，比五度相生律差异要大，为大半音。
• 从D到A的频率比是5/3*9/8=40/27(1.481481)，比纯五度（1.5）要小，为狭五度。

音乐也能作为人们唱歌的伴奏，国王今天嗓子有点不舒服，于是要求乐师把伴奏音乐降低两度（也就是本来是音E频率125改成C频率100，音C频率100改成频率80）， 不管是五度相生律还是纯率做出来的乐器，降低两度后弹奏的伴奏总是怪怪的， 直到十二平均律的出现完美的解决这个问题并尽可能的兼容了五度相生律和纯率，是音乐和数据的一个完美巧合。 下一节我们介绍我们目前通行的十二平均律。

7.十二平均律

十二平均律由中国明代音乐家朱载堉于万历十二年（1584年）首次提出，由意大利传教士利马窦传入西方。

听感差异是根据频率比来计算的，如果从频率100，乘以某个常数12次后，频率就到了200，朱载堉计算出这个常数为1.05946。

巧合的时，根据这种规则计算出来的12种音频率和五度相生律非常的吻合，比如D音一个为112.5一个为112.2462，差异为0.0514%几乎可以忽略不计。

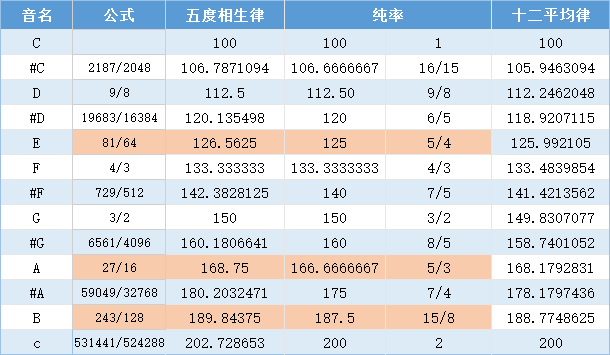
如下是三大音律频率折线图，十二平均律和五度相生律的吻合程度非常高，橙色线纯率显得和另外两个音律音差更大一些。

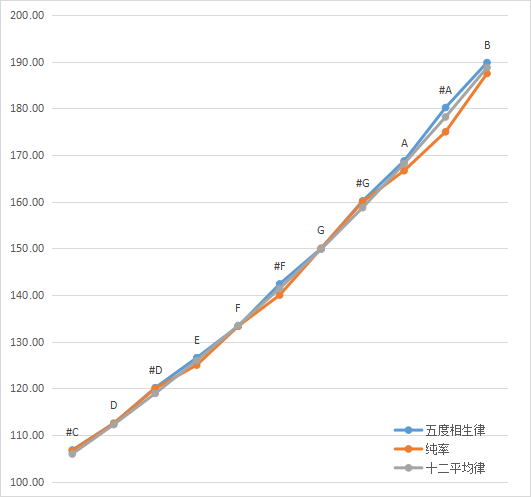
三种律法各有特点：

• 五度相生律：适用单音音乐（没有同时按几个键拨几个弦的情况），不转调移调。
• 纯率：适用于多声音乐（同时按几个键拨几个弦），不转调移调。
• 十二平均律：适用于多声音乐（同时按几个键拨几个弦）和转调移调，略有杂音（可忽略）。

8.绝对音高

三种音律只确定了各音的频率的计算方式，同样是C，不同地区在不同时期频率是不同的，比如1720年中央A在英国是380赫兹，同时期巴赫所在的德国汉堡中央A为480赫兹，不同地区的音乐和乐器互通带来很大的困难。

1939年，国际标准委员会在伦敦将a1国际标准音高（Standard ISO 16）定义为440赫兹，通过十二平均律换可以计算出其他所有音的音高，比如钢琴中央C的音高为261.6256。

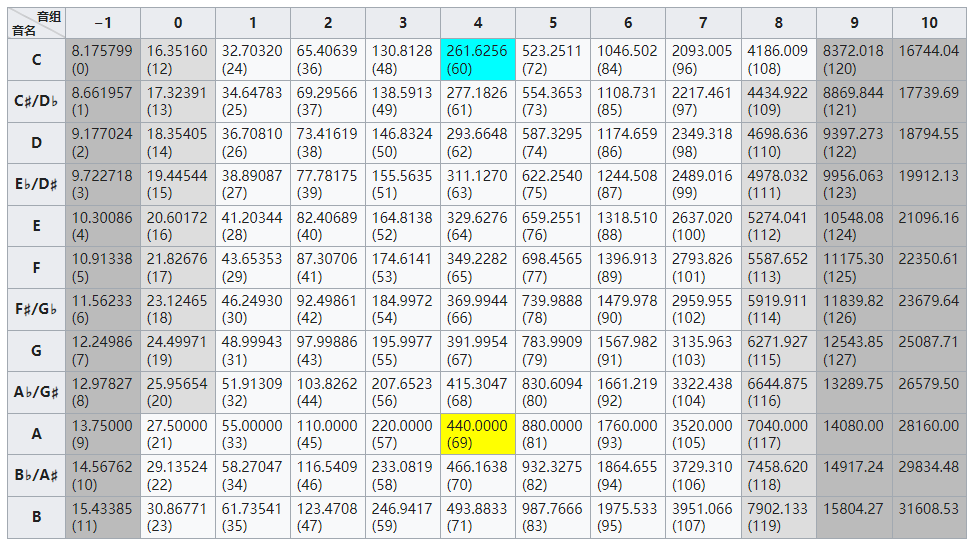
使用通行的绝对音高频率后，任何地区按照该标准制作的乐器、音响设备可以通行全球，频率下方的编号为midi电子音乐的编号。

古代音乐注重师承一大原因是频率不同，比如英国宫廷习惯听的音乐其音A为380赫兹，调律器尚未发明时民间的乐师弹奏的A频率是各不相同的，他们到宫廷演出自然听起来怪怪的难以获得认可。

9.小结

本章古人们从一根琴弦推导出12种音来制作乐器，并选择7种声音作为乐曲主要使用的音。

目前古人已经使用五度相生律制作出12个音，并使用7个音做乐曲，有些经典的曲子想要流传下来需要记录下来，另外欧洲不同城市之间的音乐交流如果总是口口相传现场演奏也不大方便。

下一章 五线谱我们讨论如何将乐曲记录到纸上并记录方式的逐步升级过程。

下一章 - 五线谱